Η υπέρβαση της δεκάδας

Ένα από τα δυσκολότερα θέματα στα Μαθηματικά της Α' Δημοτικού είναι η υπέρβαση της δεκάδας. Δηλαδή να μάθουν να προσθέτουν οι μαθητές με το μυαλό τους μονοψήφιους αριθμούς το άθροισμα των οποίων υπερβαίνει το 10, όπως 8+7 ή 9+5. Φυσικά, οι προηγούμενες προσθέσεις μπορούν να γίνουν, αν διδάξουμε στους μαθητές να ανεβαίνουν στην πρώτη περίπτωση από το 8 επτά βηματάκια και στη δεύτερη περίπτωση από το 9 πέντε βηματάκια. Είναι κι αυτός ένας τρόπος. Το θέμα όμως είναι οι μαθητές να το λύνουν αλλιώς: στην περίπτωση του 8+7 να σπάνε το 7 σε 5 και 2, το 2 να το προσθέτουν στο 8 και στο τέλος να προσθέτουν το 10 με το 5. Σε μας φαίνεται πολύ απλό· δε φαίνεται όμως στα μικρά. Κι αυτό επειδή οι μαθητές δε γνωρίζουν απέξω ότι 7=5+2 και 10=8+2. Δεν μπορούν δηλαδή εύκολα και γρήγορα να σπάνε έναν μονοψήφιο αριθμό σε δύο κομμάτια ούτε γνωρίζουν πόσα πρέπει να προσθέσεις κάθε φορά για να γίνει ένας μονοψήφιος αριθμός ίσος με το 10.

Το πρώτο βασικό στοιχείο, λοιπόν, στην πορεία για την κατάκτηση της υπέρβασης της δεκάδας είναι να μάθουν καλά τα ζευγαράκια του 10. Δηλαδή τα ζευγάρια των μονοψήφιων αριθμών των οποίων το άθροισμα ισούται με το 10. Αν τα μάθουν αυτά, μπορούν να σπάσουν τον άλλο αριθμό κάνοντας αφαίρεση. Δηλαδή στην πρόσθεση 8+7, αν ξέρεις ότι θες 2 για να φτάσεις στο 10, τότε το παιδί μπορεί στο μυαλό του να πει 7-2=5 οπότε πλέον εύκολα θα πει 10+5=15. Πώς μπορεί όμως να θυμάται τα ζευγαράκια του 10; Αν του πούμε απλώς να τα μάθει απέξω, το πιθανότερο είναι να αποτύχει. Ναι είναι μόνο 6 ζευγάρια αριθμών· μα είναι και μόνο 6 χρονών... Χρειάζεται καθημερινή εξάσκηση στην τάξη με διάφορα παιχνίδια, αν είναι δυνατόν, προκειμένου να τα μάθει.

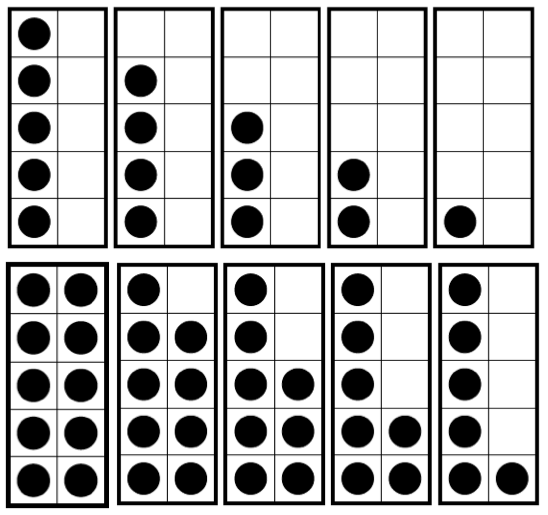
Ένας άλλος τρόπος είναι να οπτικοποιήσουμε τα ζευγάρια χρησιμοποιώντας το υλικό που φαίνεται στην εικόνα. Στα αγγλικά το ονομάζουν ten-frame, εγώ στα παιδιά το λέω «τα 10 τετραγωνάκια».

Στην παραπάνω εικόνα φαίνεται η αναπαράσταση όλων των αριθμών με το συγκεκριμένο οπτικό υλικό. Η πιο απλή άσκηση είναι, το πολύ για 5 λεπτά κάθε μέρα, να δείχνεις από μια καρτέλα στους μαθητές τη φορά κι αυτοί να λένε το νούμερο που αναπαριστά και πόσα λείπουν για να φτάσεις στο 10. Αν υπάρχει πρόσβαση σε υπολογιστές υπάρχουν 3 αντίστοιχες εφαρμογές (εδώ, εδώ κι εδώ).

Ένα επιπλέον κέρδος είναι ότι οι μαθητές μαθαίνουν τους αριθμούς και με βάση το 5. Έτσι, μπορούν να κατανοήσουν ότι το 6 είναι 5+1, το 7 είναι 5+2 κ.λ.π. Άρα, την πρόσθεση 6+7 μπορούν να την κάνουν κι αλλιώς:

6 + 7 = (5 + 1) + (5 + 2) = (5 + 5) + (1 + 2) = 10 + 3 = 13.

Προσθέσεις με βάση το 5 υπάρχουν στο βιβλίο των μαθηματικών της Α', αλλά δε νομίζω ότι παρουσιάζεται σωστά το όλο θέμα. Φυσικά, για να τους μάθουν πρέπει να εξασκηθούν. Όπως και στην προηγούμενη άσκηση, έτσι κι εδώ ο δάσκαλος πρέπει να ζητήσει από τους μαθητές να του πουν κάθε αριθμό με βάση το 5. Δηλαδή ότι το 4=5-1, 9=5+4 κ.τ.λ.

Ένα ακόμα κέρδος είναι ότι είναι δυνατόν χρησιμοποιώντας αυτό το υλικό να μάθουν και άλλες σχέσεις μεταξύ των αριθμών. Π.χ., 7=4+3=2+2+2+1, 6=4+2 κ.τ.λ. Είναι δυνατόν να χρησιμοποιηθεί και για την αναπαράσταση των δεκάδων και των μονάδων, μιας και εύκολα με το συγκεκριμένο υλικό ο μαθητής συνδέει το 10 με τη δεκάδα.

Φυσικά, δε θα τα μάθουν όλα αυτά αμέσως. Ούτε βολεύει όλους τους μαθητές. Ωστόσο, είναι ένα καλό κόλπο που λύνει προβλήματα και μυεί τους μαθητές στις σχέσεις των αριθμών. Απλώς τους θυμίζεις να σκεφτούν πώς φτιάχνουμε στα 10 τετραγωνάκια, π.χ., το 7, και αμέσως τους έρχεται στο μυαλό πόσα τους λείπουν. Και αν χρησιμοποιηθούν τα παιχνίδια στον υπολογιστή θα τους αρέσει και περισσότερο.