Ένα από τα δυσκολότερα σημεία των Μαθηματικών στην Α΄ Δημοτικού είναι οι αφαιρέσεις μεταξύ διψήφιων και μονοψήφιων, όπως το 13 - 8, 14 - 9 κ.τ.λ.
Η κλασική μέθοδος που ακολουθείται στην Ελλάδα είναι η εξής: αν έχουμε την αφαίρεση 15 - 8, αφαιρούμε πρώτα τα 5 και φτάνουμε στο 10. Στη συνέχεια, αφαιρούμε από το 8 τα 5, βρίσκουμε 3 και τα 3 τα αφαιρούμε από τα 10. Η συγκεκριμένη διαδικασία είναι πολύπλοκη και δυσνόητη. Πολλές αφαιρέσεις, πολλά πράγματα να συγκρατείς στον νου σου, δύσκολα τα πράγματα, ακόμα και αν χρησιμοποιήσεις αντικείμενα για να το εξηγήσεις.
Μια πιο απλή μέθοδος είναι η εξής: το 15 είναι φτιαγμένο από το 10 και το 5. Αφαιρείς το 8 από το 10 και το 2 που μένει το προσθέτεις με το 5. Τελείωσες! Μπορεί να φαίνεται λίγο περίεργο σε μας, αλλά για τα μικρά είναι σαφώς πιο εύκολο.
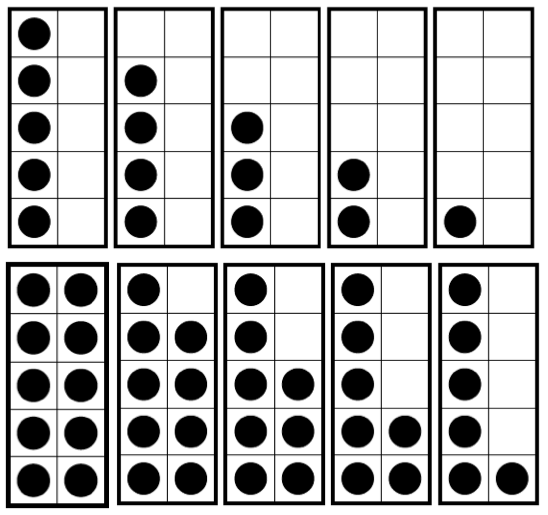
Βέβαια, στην Α΄ πρέπει να χρησιμοποιείς αντικείμενα. Θεωρώ ότι το καταλληλότερο υλικό είναι αυτό που ονομάζω «τα 10 τετραγωνάκια» και απεικονίζεται στην παρακάτω εικόνα. Αρχικά, χρησιμοποιώ 2 άδεια πλαίσια. Το πρώτο το γεμίζει ο μαθητής με 10 κυβάκια (ή ό,τι άλλο υλικό θέλετε να βάλετε) και το δεύτερο με 5. Στη συνέχεια ρωτάμε τον μαθητή από πού μπορεί να πάρει 8 κυβάκια και πόσα θα μείνουν.
Ο μαθητής βλέπει μπροστά του το 10 και το 5 και καταλαβαίνει ότι δεν είναι δυνατόν να βγάλει 8 από τα 5 αλλά μπορεί να βγάλει 8 από το 10. Βλέπει ότι κάποια περισσεύουν και πώς αυτά θα πρέπει να τα προσθέσει με τo 5. Μετά από μερικές φορές εξάσκησης με αντικείμενα θα το καταλάβει και θα μπορεί να το κάνει με τον νου του. Εννοείται ότι πάλι η ίδια διαδικασία θα ακολουθηθεί και μερικές μέρες ακόμα προκειμένου να το εμπεδώσει. Και εννοείται ότι μέχρι να τελειώσει η χρονιά θα πρέπει το παιδί να λύσει αρκετές αφαιρέσεις. Και του χρόνου στη Β΄ πάλι από την αρχή. Αυτή τη φορά όμως όλα θα κυλούν πιο γρήγορα.
Σημεία που πρέπει να προσέξει ο εκπαιδευτικός:
α) ο μαθητής πρέπει να ξέρει καλά να βρίσκει όλες τις αφαιρέσεις με μειωτέο το 10. Δεν αρκεί να ξέρει τα ζευγαράκια του 10. Θα πρέπει να ξέρει να τα χρησιμοποιεί στην αφαίρεση. Προφανώς θα πρέπει να ξέρει και τις προσθέσεις εντός του 10, προσθέσεις δηλαδή με δύο μονοψήφιους το άθροισμα των οποίων δεν υπερβαίνει το 10.
β) Στην αρχή, ο εκπαιδευτικός θα πρέπει να χρησιμοποιήσει αντικείμενα προκειμένου να καταλάβει ο μαθητής τη διαδικασία. Η κατανόηση δεν έρχεται αμέσως, ειδικά για τους αδύναμους μαθητές. Μα και όταν έρθει, το πιθανότερο είναι πως την επόμενη μέρα πάλι θα πρέπει να ξεκινήσεις από τα αντικείμενα, μετά, αν υπάρχει η δυνατότητα, να χρησιμοποιήσεις εικόνες, και στο τέλος να γράφεις μόνο την πράξη.
γ) Είναι πολύ σημαντικό οι μαθητές να ακολουθούν τις οδηγίες και να μην παίζουν με τα αντικείμενα, γιατί αλλιώς δε θα κατανοήσουν τη διαδικασία.
δ) Όταν καταλάβουν τον μηχανισμό απαιτείται πολλή εξάσκηση προκειμένου να αυτοματοποιηθεί.
ε) Στην αρχή, τα παιδά είναι δυνατόν να μπερδευτούν, ειδικά αν έχετε χρησιμοποιήσει το συγκεκριμένο υλικό για τη διδασκαλία της υπέρβασης της δεκάδας. Ένα καλό κόλπο είναι να αναδιατάξετε τα δύο πλαίσια. Αν για παράδειγμα στην υπέρβαση της δεκάδας τα είχατε το ένα δεξιά και το άλλο αριστερά, εδώ μπορείτε να βάλετε το ένα πάνω και το άλλο κάτω ή να χρησιμοποιήσετε διαφορερικό υλικό για να γεμίσετε τα τετράγωνα, ώστε να φαίνεται ότι είναι κάτι διαφορετικό.
στ) Αντί για τα «10 τετραγωνάκια» μπορεί να χρησιμοποιηθεί οποιοδήποτε άλλο υλικό. Π.χ., 2 ποτήρια όπου στο ένα να είναι συνέχεια 10 αντικείμενα — φασολάκια, καλαμάκια, ξυλάκια κ.τ.λ. — και στο άλλο όσα αντικείμενα αντιστοιχούν στις μονάδες του διψήφιου. Μπορεί, ακόμα, αντί για ποτήρια να είναι 2 κουτιά ή κάτι άλλο σχετικό. Μάλιστα καλό είναι, όταν θα γίνει επανάληψη τη δεύτερη ή την τρίτη μέρα, να χρησιμοποιηθεί και διαφορετικό υλικό.
Η κλασική μέθοδος που ακολουθείται στην Ελλάδα είναι η εξής: αν έχουμε την αφαίρεση 15 - 8, αφαιρούμε πρώτα τα 5 και φτάνουμε στο 10. Στη συνέχεια, αφαιρούμε από το 8 τα 5, βρίσκουμε 3 και τα 3 τα αφαιρούμε από τα 10. Η συγκεκριμένη διαδικασία είναι πολύπλοκη και δυσνόητη. Πολλές αφαιρέσεις, πολλά πράγματα να συγκρατείς στον νου σου, δύσκολα τα πράγματα, ακόμα και αν χρησιμοποιήσεις αντικείμενα για να το εξηγήσεις.
Μια πιο απλή μέθοδος είναι η εξής: το 15 είναι φτιαγμένο από το 10 και το 5. Αφαιρείς το 8 από το 10 και το 2 που μένει το προσθέτεις με το 5. Τελείωσες! Μπορεί να φαίνεται λίγο περίεργο σε μας, αλλά για τα μικρά είναι σαφώς πιο εύκολο.
Βέβαια, στην Α΄ πρέπει να χρησιμοποιείς αντικείμενα. Θεωρώ ότι το καταλληλότερο υλικό είναι αυτό που ονομάζω «τα 10 τετραγωνάκια» και απεικονίζεται στην παρακάτω εικόνα. Αρχικά, χρησιμοποιώ 2 άδεια πλαίσια. Το πρώτο το γεμίζει ο μαθητής με 10 κυβάκια (ή ό,τι άλλο υλικό θέλετε να βάλετε) και το δεύτερο με 5. Στη συνέχεια ρωτάμε τον μαθητή από πού μπορεί να πάρει 8 κυβάκια και πόσα θα μείνουν.
Σημεία που πρέπει να προσέξει ο εκπαιδευτικός:
α) ο μαθητής πρέπει να ξέρει καλά να βρίσκει όλες τις αφαιρέσεις με μειωτέο το 10. Δεν αρκεί να ξέρει τα ζευγαράκια του 10. Θα πρέπει να ξέρει να τα χρησιμοποιεί στην αφαίρεση. Προφανώς θα πρέπει να ξέρει και τις προσθέσεις εντός του 10, προσθέσεις δηλαδή με δύο μονοψήφιους το άθροισμα των οποίων δεν υπερβαίνει το 10.
β) Στην αρχή, ο εκπαιδευτικός θα πρέπει να χρησιμοποιήσει αντικείμενα προκειμένου να καταλάβει ο μαθητής τη διαδικασία. Η κατανόηση δεν έρχεται αμέσως, ειδικά για τους αδύναμους μαθητές. Μα και όταν έρθει, το πιθανότερο είναι πως την επόμενη μέρα πάλι θα πρέπει να ξεκινήσεις από τα αντικείμενα, μετά, αν υπάρχει η δυνατότητα, να χρησιμοποιήσεις εικόνες, και στο τέλος να γράφεις μόνο την πράξη.
γ) Είναι πολύ σημαντικό οι μαθητές να ακολουθούν τις οδηγίες και να μην παίζουν με τα αντικείμενα, γιατί αλλιώς δε θα κατανοήσουν τη διαδικασία.
δ) Όταν καταλάβουν τον μηχανισμό απαιτείται πολλή εξάσκηση προκειμένου να αυτοματοποιηθεί.
ε) Στην αρχή, τα παιδά είναι δυνατόν να μπερδευτούν, ειδικά αν έχετε χρησιμοποιήσει το συγκεκριμένο υλικό για τη διδασκαλία της υπέρβασης της δεκάδας. Ένα καλό κόλπο είναι να αναδιατάξετε τα δύο πλαίσια. Αν για παράδειγμα στην υπέρβαση της δεκάδας τα είχατε το ένα δεξιά και το άλλο αριστερά, εδώ μπορείτε να βάλετε το ένα πάνω και το άλλο κάτω ή να χρησιμοποιήσετε διαφορερικό υλικό για να γεμίσετε τα τετράγωνα, ώστε να φαίνεται ότι είναι κάτι διαφορετικό.
στ) Αντί για τα «10 τετραγωνάκια» μπορεί να χρησιμοποιηθεί οποιοδήποτε άλλο υλικό. Π.χ., 2 ποτήρια όπου στο ένα να είναι συνέχεια 10 αντικείμενα — φασολάκια, καλαμάκια, ξυλάκια κ.τ.λ. — και στο άλλο όσα αντικείμενα αντιστοιχούν στις μονάδες του διψήφιου. Μπορεί, ακόμα, αντί για ποτήρια να είναι 2 κουτιά ή κάτι άλλο σχετικό. Μάλιστα καλό είναι, όταν θα γίνει επανάληψη τη δεύτερη ή την τρίτη μέρα, να χρησιμοποιηθεί και διαφορετικό υλικό.
Σχόλια