Πιθανότατα ο καλύτερος τρόπος για να σχολιάσεις τα αποτελέσματα της αξιολόγησης Pisa είναι να δεις τι ζητείται από τους μαθητές. Σε αυτόν τον σύνδεσμο υπάρχουν ενδεικτικά προβλήματα Μαθηματικών. Αν κάποιος τα διαβάσει όλα, μάλλον θα καταλήξει στο εξής συμπέρασμα: η συστηματικά χαμηλή βαθμολογία των Ελλήνων μαθητών οφείλεται στο ότι στο ελληνικό σχολείο δε διδάσκονται τα Μαθηματικά που απαιτούνται για να λύσουν τα συγκεκριμένα προβλήματα. Είτε δεν είναι στην ύλη είτε καταλαμβάνουν πολύ μικρό ποσοστό της κι επομένως ο χρόνος που αφιερώνεται είναι ανεπαρκής, με αποτέλεσμα οι μαθητές να αποτυγχάνουν.
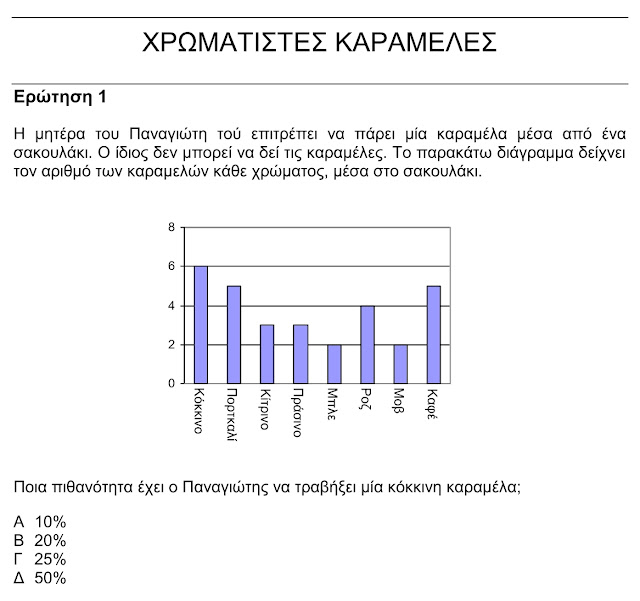
Ενδεικτικό είναι το προτελευταίο πρόβλημα, οι «Χρωματιστές καραμέλες». Πρόκειται για ένα απίστευτα εύκολο πρόβλημα που πραγματικά απορώ γιατί το έβαλαν. Το μόνο που χρειάζεται για να το λύσεις είναι να έχεις διδαχτεί στο σχολείο συστηματικά τις πιθανότητες. Πότε όμως διδαχτήκαμε στο σχολείο συστηματικά τις πιθανότητες; Ποτέ! Συνεπώς πώς είναι δυνατόν να περιμένουμε ότι σε μία πολύωρη εξέταση με πληθώρα ερωτήσεων οι 15χρονοι μαθητές ξαφνικά θα ανακαλύψουν από το μηδέν την έννοια της πιθανότητας και θα απαντήσουν σωστά το συγκεκριμένο πρόβλημα;
Ένα άλλο πολύ απλό πρόβλημα είναι τα «Σχήματα». Η λύση, όμως, είναι αυτονόητη μόνο αν έχεις διδαχτεί πώς να λύνεις τέτοια προβλήματα. Αν δεν το έχεις διδαχτεί δεν έχεις καμία ελπίδα να το λύσεις, ειδικά αν είσαι 15 χρονών, συμμετέχεις σε έναν αδιάφορο για σένα διαγωνισμό στον οποίο πρέπει να απαντήσεις πάρα πολλές ερωτήσεις σε τρία διαφορετικά γνωστικά αντικείμενα. Και οι ίδιοι οι μαθηματικοί ακόμα που πρωτοέλυσαν αυτό το πρόβλημα δεν έπρεπε παράλληλα να λύσουν πολλά ακόμα μαθηματικά προβλήματα, να απαντήσουν σε πολλές ερωτήσεις κατανόησης κειμένου και να αντιμετωπίσουν πολλά θέματα φυσικών επιστημών σε περιορισμένο χρονικό περιθώριο. Τα 15χρονα θα το καταφέρουν;
Γενικά όποιος έχει την υπομονή και διαβάσει το σύνολο των προβλημάτων, ενώ ταυτόχρονα γνωρίζει και την ύλη των Μαθηματικών του ελληνικού σχολείου, θα διαπιστώσει ότι σχεδόν όλα είναι εκτός ύλης. Επειδή έχω δει διάφορες ερμηνείες των συστηματικά χαμηλών επιδόσεων των Ελλήνων μαθητών, να πω τα εξής: και καλύτερους εκπαιδευτικούς να αποκτήσουμε και περισσότερα λεφτά να ρίξουμε στα σχολεία και να αξιολογήσουμε αυστηρά σχολεία και εκπαιδευτικούς, από τη στιγμή που τα θέματα είναι εκτός ύλης, οι μαθητές πάλι δε θα τα λύσουν. Στα σχολεία διδάσκεται συγκεκριμένη ύλη που δεν καθορίζεται από την ποιότητα των εκπαιδευτικών, τον προϋπολογισμό του κράτους ή την αξιολόγηση. Η μόνη λύση που απομένει είναι να κάνουμε στην άκρη τα Μαθηματικά που διδάσκουμε τώρα και να βάλουμε στο σχολείο αυτά που εξετάζονται στη συγκεκριμένη αξιολόγηση. Είναι όμως τόσο απλά τα πράγματα;
Αν εφαρμόσουμε αυτήν την πολιτική θα παραγκωνίσουμε την Άλγεβρα. Χωρίς να είμαι ειδικός και με βάση όσα καταλαβαίνω, αν κάνουμε στην άκρη την Άλγεβρα του Γυμνασίου, οι μαθητές δε θα μπορούν να μάθουν τα Μαθηματικά που διδάσκονται αυτήν τη στιγμή στο Λύκειο και πιθανότατα θα αντιμετωπίσουν δυσκολίες και στο μάθημα της Φυσικής. Η Άλγεβρα που διδάσκεται στο Λύκειο είναι απολύτως απαραίτητη για τις σχολές του Πολυτεχνείου και των Θετικών Επιστημών. Αν έχω δίκιο σε όσα προαναφέρω πώς αντιμετωπίζεται αυτό το πρόβλημα; Μήπως αν ακολουθήσουμε αυτήν την τακτική θα αντικαταστήσουμε ένα πρόβλημα με ένα άλλο; Και τελικά το θέμα μας είναι να πάμε καλά σε έναν διαγωνισμό 15χρονων ή να βελτιώσουμε τη διδασκαλία των Μαθηματικών;
ΥΓ 1: σε αυτόν τον σύνδεσμο υπάρχουν θέματα τελικών εξετάσεων Μαθηματικών Α Λυκείου. Δε χρειάζεται να ξέρει κάποιος Μαθηματικά για να καταλάβει τις τεράστιες διαφορές των θεμάτων.
ΥΓ 2: σε αυτό το άρθρο η υπεύθυνη της συγκεκριμένης αξιολόγησης στην ελλάδα αναφέρει μεταξύ άλλων τα εξής: «Ουσιαστικά, το PISA εξετάζει δύο πράγματα: να έχεις τις γνώσεις αλλά κυρίως, να ξέρεις να τις χρησιμοποιείς. Για παράδειγμα, δεν αρκεί να γνωρίζεις ένα μαθηματικό τύπο αλλά πρέπει να ξέρεις και πώς αυτός μπορεί να χρησιμοποιηθεί. Η εικόνα των Ελλήνων μαθητών θα ήταν οπωσδήποτε διαφορετική και θα εμφάνιζαν πολύ μεγαλύτερα ποσοστά επιτυχίας, εάν το PISA έδινε ένα θέμα καθαρά θεωρητικό, όπως ένα τύπο στα Μαθηματικά ή στη Φυσική. Ζητώντας, δηλαδή, από ένα μαθητή να βρει "αν ένα σφαιρίδιο βάλλεται από ένα σημείο Α προς ένα σημείο Β με τόση ταχύτητα, ποια είναι η ορμή" μπορεί να τη βρει. Αν του πεις "ο Γιάννης πετάει τη μπάλα στη Μαρία με τόση ταχύτητα", εκεί δεν μπορεί να τη βρει».


Σχόλια